Efficient event-based delay learning
Myelination
The brain enables the organism to learn and change behavior to an ever-changing environement. Most studies try to understand the underpinnings of plasticy through synaptic weight changes. Myelin however is also plastic and there has been experimental evidence that shows that similary to synaptic strength, it is modulated by neuron activity
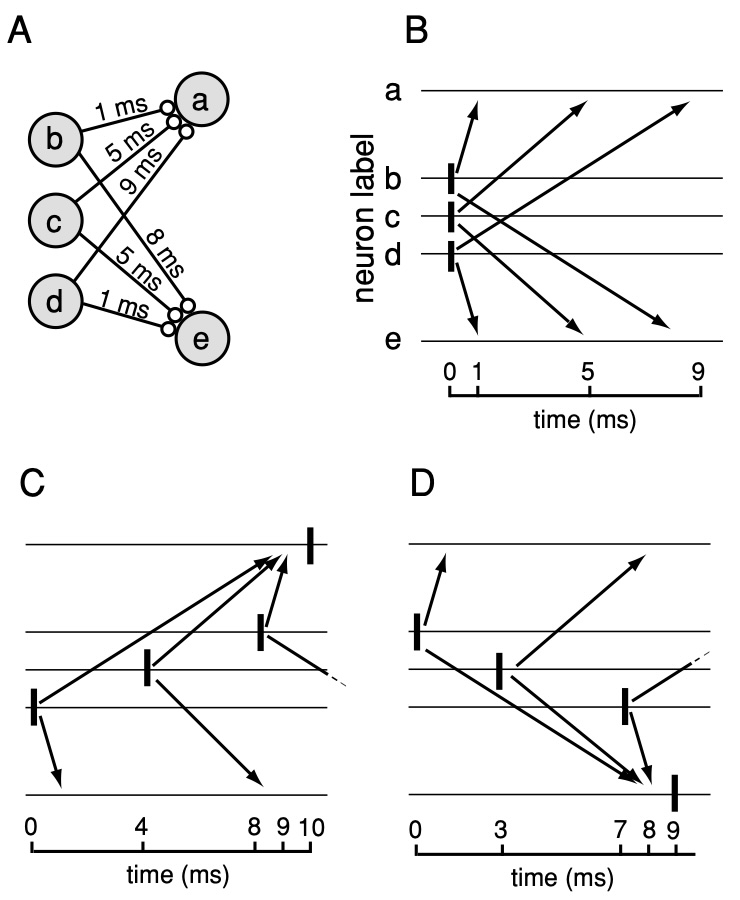
How could we study the benefits of myelin plascitcity in artificial neural networks? One option is introducing optimisable delays in Spiking Neural Networks.
Delay learning
We are the not the first to be interested in employing such mechanisms into machine learning setups. There has been a recent upsurge in interest since Hammouamri et. al.
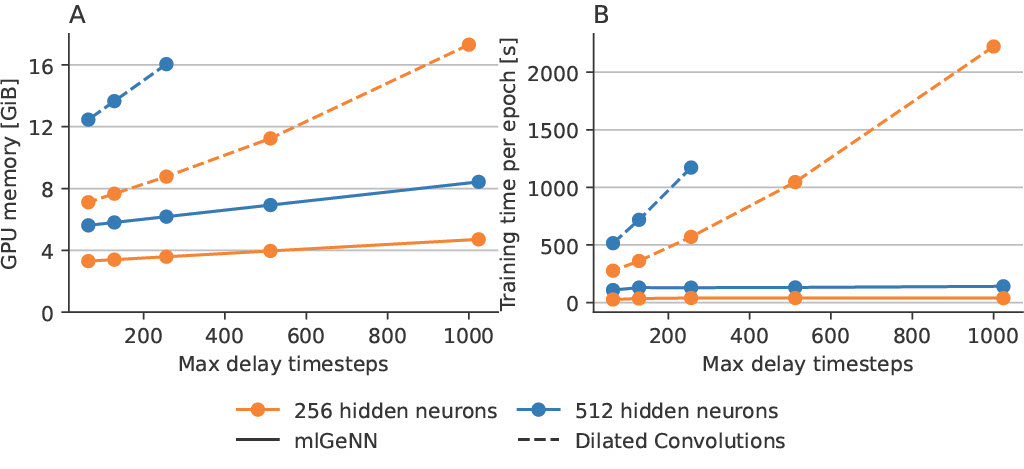
A major drawback to their method lies in the ammeanability for neuromorphic hardware. While for inference discretising the whole network is not necessarily an issue, for training every timestep needs to be stored in the memory, which limits both networks size and temporal precisions and/or sequence length. This is an issue that is general to backpropagation through time (BPTT).
Wunderlich et. al.
Results
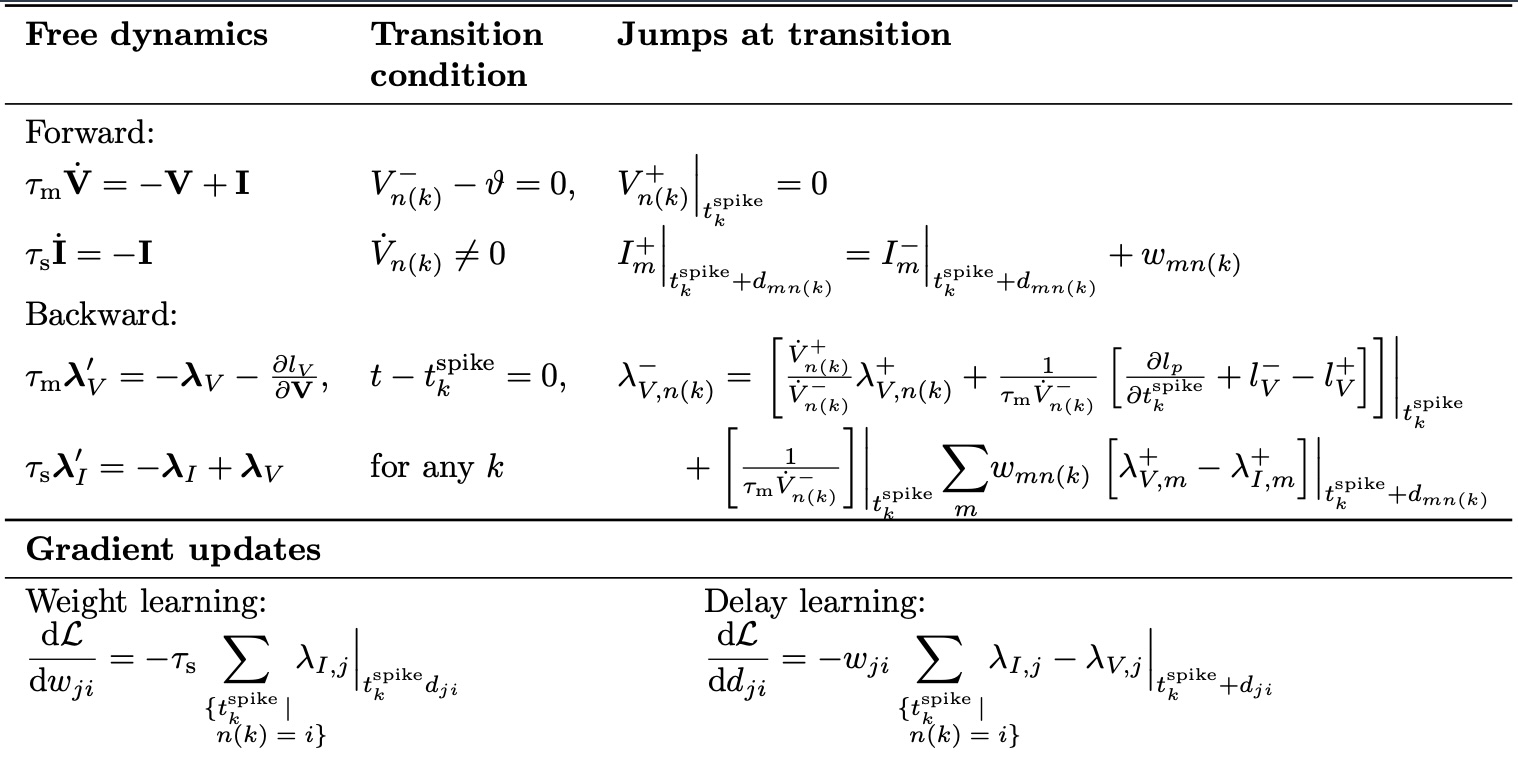
After extensive calculations
We test our implementations on the Yin-yang, Spiking Heidelberg Digits, Spiking Speech Commands, and Braille letter reading datasets. We find the delays are always a useful addition, and interestingly, they become particularly useful in small recurrent networks.
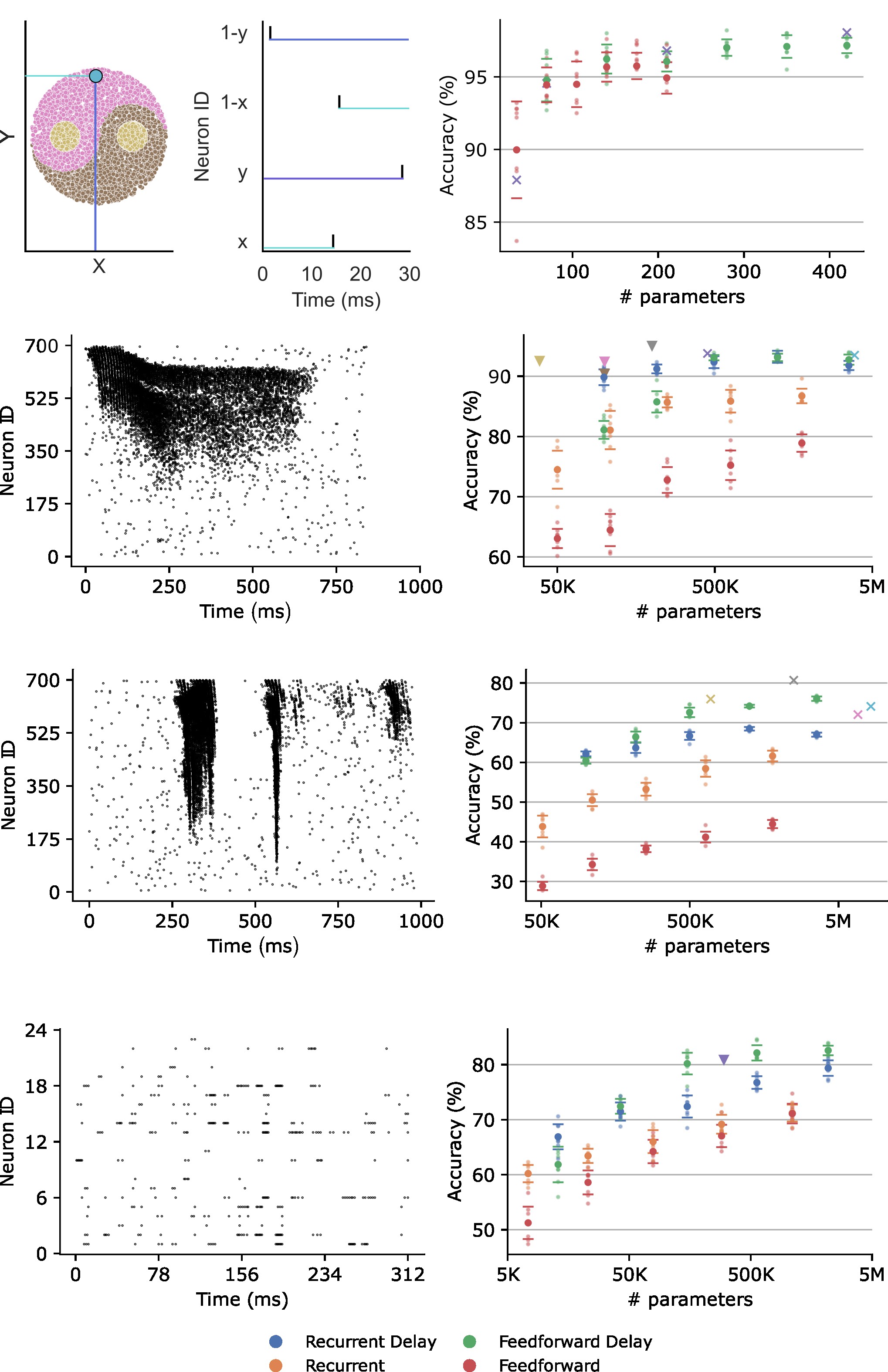
With the correct implementations this method becomes significantly more efficient than discretisaiton (i.e BPTT) based methods. With fixed network sizes and maximum delay timesteps, we outperform the DCLS based method both in terms of memory requirements in speed.
We also tested our method on Loihi 2 for inference